 Reglas de derivación
Reglas de derivación

Derivada de una potencia real
Una función exponencial con
exponente real se representa por f(x)=xn y su derivada es f'(x)=nx^{n-1}..
Por ejemplo
tomemos la función:
f(x)=x^{3}
Lo primero que se debe hacer es
"bajar" el exponente de tal forma que éste multiplique a la variable
con respecto a la cual estamos derivando, luego al mismo exponente se le resta
la unidad formando uno nuevo, así:
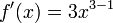
Quedando
finalmente:
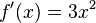
Considérese
la función 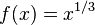
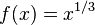
Se tiene:
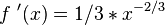
Derivada de una constante por una función
Cuando
una función esté representada por medio de 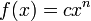 , su derivada equivale a
, su derivada equivale a  de la siguiente manera:
de la siguiente manera:
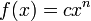 , su derivada equivale a
, su derivada equivale a  de la siguiente manera:
de la siguiente manera:
Consideremos
la siguiente función:
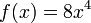 ,
,
lo primero a hacer es "bajar" al
exponente a multiplicar por la variable y el coeficiente que la acompaña, y de
nuevo se halla un nuevo exponente de la misma manera explicada anteriormente:

Para obtener
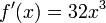
Cuando una constante acompaña a una variable cuyo
exponente es 1 su derivada será el valor de la constante:
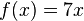
Entonces su derivada con respecto a esta variable
será:
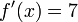
Puesto
que 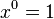
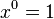
Derivada de una suma
Se puede demostrar a partir de la definición de derivada, que la
derivada de la suma de dos funciones es la suma de las derivadas de cada una.
Es decir,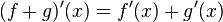 o
o ![\frac{d[f(x)+g(x)]}{dx}=\frac{df}{dx}+\frac{dg}{dx}](http://upload.wikimedia.org/math/7/1/5/7151a57c6b721f3f59162f9cf4db47d6.png) .
.
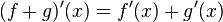 o
o ![\frac{d[f(x)+g(x)]}{dx}=\frac{df}{dx}+\frac{dg}{dx}](http://upload.wikimedia.org/math/7/1/5/7151a57c6b721f3f59162f9cf4db47d6.png) .
.
Como ejemplo consideremos la función:  , para determinar su derivada se trabaja la
derivada de cada término aparte y la suma de ambos será la derivada de la
función:
, para determinar su derivada se trabaja la
derivada de cada término aparte y la suma de ambos será la derivada de la
función:
 , para determinar su derivada se trabaja la
derivada de cada término aparte y la suma de ambos será la derivada de la
función:
, para determinar su derivada se trabaja la
derivada de cada término aparte y la suma de ambos será la derivada de la
función: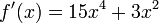
Derivada de un producto
La derivada se expresa literalmente de la siguiente forma:
"La derivada de un producto de
dos funciones es equivalente a la suma entre el producto de la primera función
sin derivar y la derivada de la segunda función y el producto de la derivada de
la primera función por la segunda función"
Y matemáticamente expresado por la relación 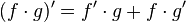 .Consideremos la
siguiente función como ejemplo:
.Consideremos la
siguiente función como ejemplo: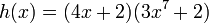
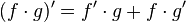 .Consideremos la
siguiente función como ejemplo:
.Consideremos la
siguiente función como ejemplo: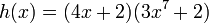
Identificamos a  y
y 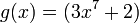 ,
utilizando las reglas anteriormente expuestas, vemos que:
,
utilizando las reglas anteriormente expuestas, vemos que:
 y
y 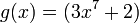 ,
utilizando las reglas anteriormente expuestas, vemos que:
,
utilizando las reglas anteriormente expuestas, vemos que: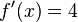 y que
y que 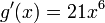
Por lo tanto
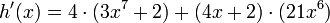
Simplificando y organizando el
producto obtenido nos queda:
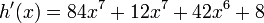
Sumamos términos semejantes y
finalmente obtenemos la derivada:

Si por ejemplo tenemos la derivada
del producto de tres funciones que dependen de la misma variable, podemos
pensar el producto de dos de las funciones como si se tratara de una tercera función
es decir 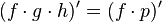 en donde
en donde 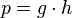 (sin importar que dos funciones
escogemos).
(sin importar que dos funciones
escogemos).
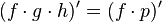 en donde
en donde 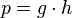 (sin importar que dos funciones
escogemos).
(sin importar que dos funciones
escogemos).
Integrales Definidas
·
Concepto
Histórico Desde su origen, la noción de integral ha respondido a la necesidad
de mejorar los métodos de medición de áreas subtendidas bajo líneas y
superficies curvas. La técnica de integración se desarrolló sobre todo a partir
del siglo XVII, paralelamente a los avances que tuvieron lugar en las teorías
sobre derivadas y en el cálculo diferencial.
·
Definición de Integral Definida La integral
definida es un concepto utilizado para determinar el valor de las áreas
limitadas por curvas y rectas. Dado el intervalo [a, b] en el que, para cada
uno de sus puntos x, se define una función f (x) que es mayor o igual que 0 en
[a, b], se llama integral definida de la función entre los puntos a y b al área
de la porción del plano que está limitada por la función, el eje horizontal OX
y las rectas verticales de ecuaciones x = a y x = b.
INTEGRALES INDEFINIDAS
Usted está
familiarizado con algunas operaciones
inversas. La adición y la sustracción son operaciones inversas,
la multiplicación y la división son también operaciones inversas, así como la
potenciación y la extracción de raíces. Ahora, conocerá la operación inversa la
de derivación o diferenciación denominada antiderivación o antidiferenciación, la cual implica el cálculo de una antiderivada.
Antiderivada.
Una función F se
denomina antiderivada de
una función f en un intervalo I si  para
todo
para
todo 
 para
todo
para
todo 
Ejemplo.
Si F es
la función definida por  entonces
entonces  De
modo que si
De
modo que si  entonces f es
la derivada de F, y F es la antiderivada de f.
Si G es la función definida por
entonces f es
la derivada de F, y F es la antiderivada de f.
Si G es la función definida por  entonces G también
es una antiderivada de f, porque
entonces G también
es una antiderivada de f, porque  En
realidad, cualquier función H definida por
En
realidad, cualquier función H definida por  donde C es
una constante, es una antiderivada de f.
donde C es
una constante, es una antiderivada de f.
 entonces
entonces  De
modo que si
De
modo que si  entonces f es
la derivada de F, y F es la antiderivada de f.
Si G es la función definida por
entonces f es
la derivada de F, y F es la antiderivada de f.
Si G es la función definida por  entonces G también
es una antiderivada de f, porque
entonces G también
es una antiderivada de f, porque  En
realidad, cualquier función H definida por
En
realidad, cualquier función H definida por  donde C es
una constante, es una antiderivada de f.
donde C es
una constante, es una antiderivada de f.
Teorema 1.
Si f y g son
dos funciones definidas
en el intervalo I, tales que  para
todo
para
todo  entonces
existe una constante K tal que
entonces
existe una constante K tal que  para
todo
para
todo 
 para
todo
para
todo  entonces
existe una constante K tal que
entonces
existe una constante K tal que  para
todo
para
todo 
"La antiderivación o antidiferenciación es el proceso mediante
el cual se determina el conjunto de todas las antiderivadas de una función
dada. El símbolo  denota la operación de antiderivación, y se
escribe donde
denota la operación de antiderivación, y se
escribe donde  y
y 
 denota la operación de antiderivación, y se
escribe donde
denota la operación de antiderivación, y se
escribe donde  y
y 
En la
igualdad  x es
la variable de integración,
x es
la variable de integración,  es
el integrando y la expresión
es
el integrando y la expresión  recibe
el nombre de antiderivada general o integral indefinida de f.
Si
recibe
el nombre de antiderivada general o integral indefinida de f.
Si  es
el conjunto de todas las funciones cuyas diferenciales sean
es
el conjunto de todas las funciones cuyas diferenciales sean  también
es el conjunto de todas las funciones cuya derivada es
también
es el conjunto de todas las funciones cuya derivada es 
 x es
la variable de integración,
x es
la variable de integración,  es
el integrando y la expresión
es
el integrando y la expresión  recibe
el nombre de antiderivada general o integral indefinida de f.
Si
recibe
el nombre de antiderivada general o integral indefinida de f.
Si  es
el conjunto de todas las funciones cuyas diferenciales sean
es
el conjunto de todas las funciones cuyas diferenciales sean  también
es el conjunto de todas las funciones cuya derivada es
también
es el conjunto de todas las funciones cuya derivada es 
Teorema 2.

Teorema 3.

donde a es una
constante.
Teorema 4.
Si las
funciones f y g están definidas en el mismo
intervalo, entonces 

Teorema 5.
Si las
funciones  están
definidas en el mismo intervalo, entonces
están
definidas en el mismo intervalo, entonces 
 están
definidas en el mismo intervalo, entonces
están
definidas en el mismo intervalo, entonces 
donde  son
constantes.
son
constantes.
 son
constantes.
son
constantes.
Teorema 6.
Si n es
un número racional, entonces 

Ejemplos.
1) Evalúe 

Solución.

2) Calcule 

Solución.

3) Determine 

Solución.

Los teoremas
para las integrales indefinidas
de las funciones trigonométricas seno, coseno, secante al cuadrado, cosecante
al cuadrado, secante por tangente y cosecante por cotangente, son deducciones
inmediatas de los teoremas correspondientes de diferenciación. A continuación
se presentan tales teoremas.
Ecuación
Una ecuación es una igualdad matemática entre
dos expresiones algebraicas, denominadas miembros, en las que aparecen valores
conocidos o datos, y desconocidos o incógnitas, relacionados mediante
operaciones matemáticas. nota 1 Los valores conocidos pueden ser números,
coeficientes o constantes; y también variables cuya magnitud pueda ser
establecida a través de las restantes ecuaciones de un sistema, o bien mediante
otros procesos. nota 2 [cita requerida] Las incógnitas, representadas
generalmente por letras, constituyen los valores que se pretende hallar. Por
ejemplo, en la ecuación:

la variable X representa la incógnita, mientras que
el coeficiente 3 y los números 1 y 9 son constantes conocidas. La igualdad
planteada por una ecuación será cierta o falsa dependiendo de los valores
numéricos que tomen las incógnitas; se puede afirmar entonces que una ecuación
es una igualdad condicional,
en la que sólo ciertos valores de las variables (incógnitas) la hacen cierta.
Se llama solución de una ecuación a cualquier valor
individual de dichas variables que la satisfaga. Para el caso dado, la solución
es:
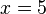
Resolver una ecuación es encontrar su dominio
solución, que es el conjunto de valores de las incógnitas para los cuales la
igualdad se cumple. Por lo general, los problemas matemáticos pueden expresarse
en forma de una o más ecuaciones;[cita requerida] sin embargo no todas las
ecuaciones tienen solución, ya que es posible que no exista ningún valor de la
incógnita que haga cierta una igualdad dada. En ese caso, el conjunto de
soluciones de la ecuación será vacío y se dice que la ecuación no es resoluble.
De igual modo, puede tener un único valor, o varios, o incluso infinitos
valores, siendo cada uno de ellos una solución particular de la ecuación. Si
cualquier valor de la incógnita hace cumplir la igualdad (esto es, no existe
ningún valor para el cual no se cumpla) la ecuación es en realidad una
identidad. nota 3
La ciencia utiliza ecuaciones para enunciar
de forma precisa leyes; estas ecuaciones expresan relaciones entre variables.
Así, en física, la ecuación de la dinámica de Newton relaciona las variables
fuerza F, aceleración a y masa m: F = ma. Los valores que son solución de la
ecuación anterior cumplen la primera ley de la mecánica de Newton. Por ejemplo,
si se considera una masa m = 1 kg y una aceleración a = 1 m/s, la única solución
de la ecuación es F = 1 kg·m/s = 1 Newton, que es el único valor para la fuerza
permitida por la ley.
Ejemplos:
El campo de aplicación de las ecuaciones es
inmenso, y por ello hay una gran cantidad de investigadores dedicados a su
estudio.
Tipos de ecuaciones
Las ecuaciones pueden clasificarse según el
tipo de operaciones necesarias para definirlas y según el conjunto de números
sobre el que se busca la solución. Entre los tipos más frecuentes están:
- Ecuaciones algebraicas
- Ecuaciones trascendentes, cuando involucran funciones no polinómicas, como las funciones trigonométricas, exponenciales, logarítmicas.
- Ecuaciones diferenciales
- Ecuaciones integrales
- Ecuaciones funcionales
NOTA: DARLE CLIC A LAS PALABRAS ROJAS Y O AZUL PARA OBTENER MAS INFORMACIÓN.
